SIR Model Basics Background

In this section, you will learn about a common epidemiological model called the SIR model. You’ll then use a simulator based on this model to explore a short disease outbreak in a small population.

Sometimes called “epidemic models.” These models are tools used to understand and predict the spread of infectious diseases in populations. They are often developed by scientists and mathematicians based on available data.

Epidemiological models are often built using mathematical modeling: a process that uses mathematical equations to represent a real-world system or scenario. Mathematical models can be used to make predictions, analyze results, and provide insights about real-world problems.

What is an SIR model?

An SIR model simulates the spread of an infectious disease in a population. "SIR” stands for the three main groups in the model: Susceptible, Infectious, and Removed.

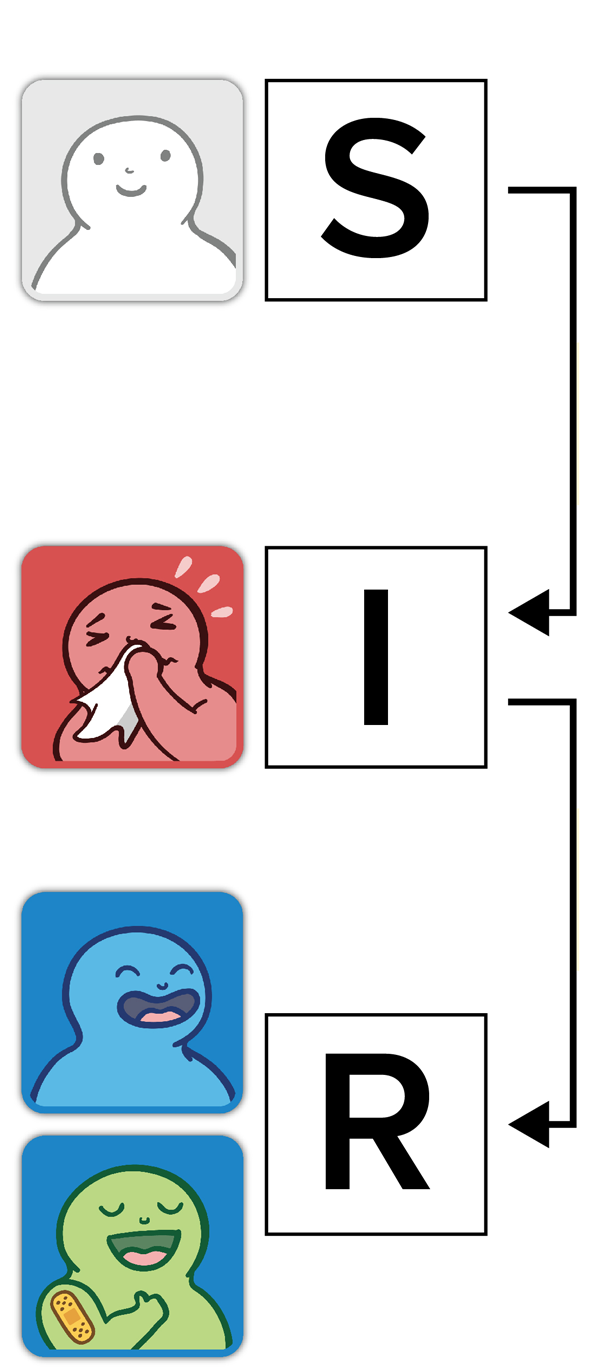
A flow diagram of the S-I-R model, showing the stages that individuals pass through from Susceptible to Infectious to Removed.

Susceptible

Uninfected and unvaccinated individuals who can become infected

Transmission

The process by which susceptible individuals become infected

Infectious

Individuals who are infected with a given pathogen and can pass the pathogen to susceptible individuals

Recovery

The process by which infected individuals recover

Removed

  1. Individuals who were infected but have recovered, and are now immune (cannot be reinfected)
  2. Individuals who are vaccinated and are now immune
In the SIR model, the population is divided into three distinct groups: susceptible individuals, infectious individuals, and removed individuals. As individuals become infected, they move from the susceptible group to the infectious group based on transmission. As individuals recover, they move from the infectious group to the removed group based on recovery. The removed group also includes vaccinated individuals who cannot become infected in this model.

The SIR model is dynamic, meaning that the number of individuals in each group changes over time. You can use the model to predict the number of susceptible, infectious, and removed individuals in a population at specific timepoints.

Watch this video describing the SIR model.

Detailed description of the SIR model.

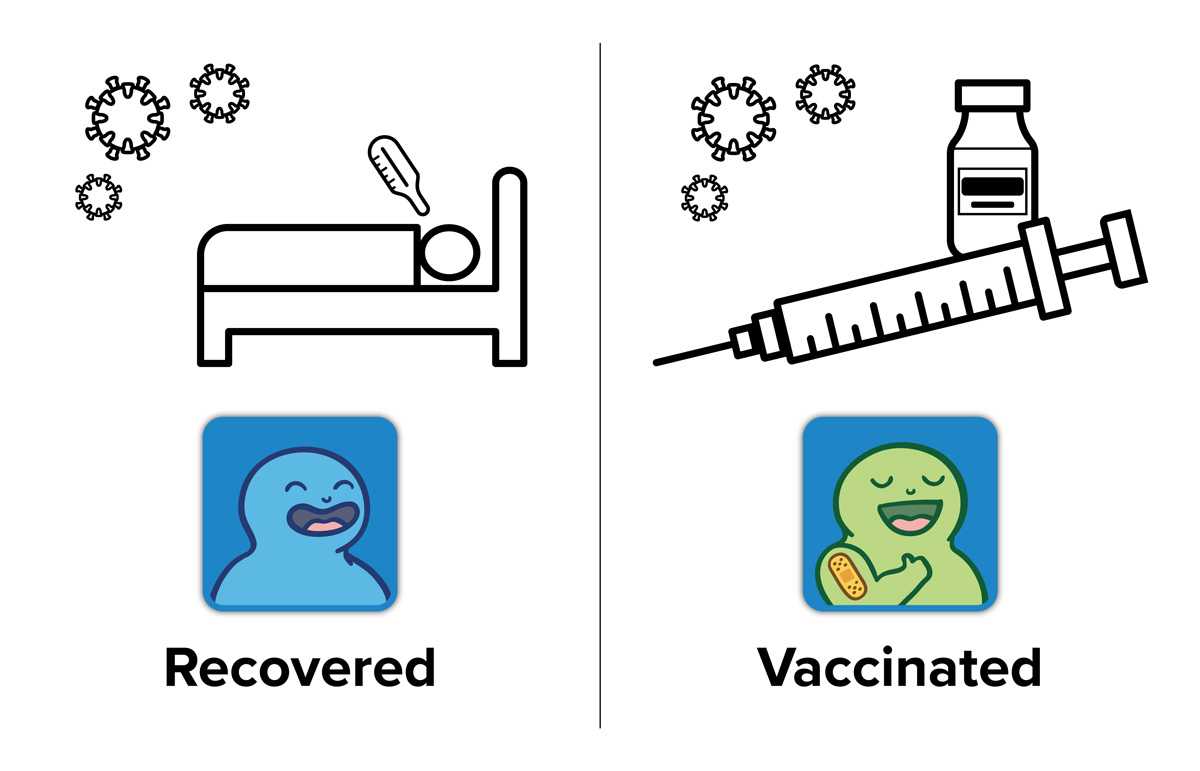
Removed Group Has Immunity

Individuals in the removed group have immunity against the pathogen, which protects them from becoming infected. They gain immunity after recovering from a previous infection or through vaccination.

The body’s ability to effectively recognize and destroy certain pathogens. When an individual has immunity against a pathogen (also called being immune), they cannot be infected by that pathogen.

Vaccinated individuals have received a vaccine against a specific pathogen. If a vaccinated individual encounters the same pathogen at another time, their body can recognize and destroy the pathogen more quickly than if they had not been vaccinated.

A substance, typically injected into the body, that helps an individual develop immunity against a pathogen. Vaccines work by triggering the body’s response against the pathogen without causing disease. The body is then better prepared to recognize and destroy the same type of pathogen in the future.
The icons for recovered and vaccinated individuals.
Individuals in the removed group gain immunity through recovery from infection or through vaccination.

Assumptions in Modeling

All models are based on assumptions: conditions we treat as true, including simplifications we make about the world or system we are studying. Although not all assumptions are true in real life, they can make a model easier to build, understand, and analyze.

Our SIR model makes some assumptions, including:

Three Groups

The population is divided into three distinct groups: susceptible individuals, infectious individuals, and removed individuals.

Population Doesn’t Increase

The total population never increases (e.g., no births or individuals moving into the population).

Transmission

When infectious and susceptible individuals interact, those susceptible individuals (called close contacts) may become infected. Once infected, they are immediately infectious and can spread the pathogen to others.

Population Doesn’t Decrease

The total population never decreases (e.g., no deaths or individuals moving out of the population).

No Reinfection

Once someone recovers, they are immune and cannot become reinfected (they will not reenter the susceptible group).

Equal Number of Contacts

All individuals interact with equal numbers of other individuals.

Not all the assumptions in our SIR model are true of real-world populations. For example, although our model says there are no reinfections, reinfections can occur for real diseases like the flu. Other versions of the SIR model may make different assumptions that more closely mimic the real world.

In the “Tutorial,” you will learn the basic processes that an SIR model uses to simulate daily disease spread, as well as some more assumptions of our model. You will then simulate an infectious disease outbreak in a small population, collect data, and generate a graph.

Continue to Tutorial